Introduction

Historical Remarks

Muqarnas is the Arabic word for stalactite vault, an architectural ornament developed around the middle of the tenth century in north eastern Iran and almost simultaneously, but apparently independently, in central North Africa.
Two points about these new forms are of importance. One is that, from the late eleventh century on, all Muslim lands adopted and developed the muqarnas, which became almost as common a feature of an elevation as the Corinthian capital was in Antiquity. The second and far more important point is that, from the moment of its first appearance, the muqarnas acquired four characteristic attributes, whose evolution and characteristics form its history: it was three-dimensional and therefore provided volume wherever it was used, the nature and depth of the volume being left to the discretion of the maker; it could be used both as an architectonic form, because of its relationship to vaults, and as an applied ornament, because its depth could be controlled; it had no intrinsic limits, since not one of its elements is a finite unit of composition and there is no logical or mathematical limitation to the scale of any one composition; and it was a three-dimensional unit which could be resolved into a two-dimensional outline.
The fifteenth century Timurid mathematician Ghiyath al-Din Mas'ud al-Kashi (~1380 - 1429) defines the muqarnas in his practical way as: "The muqarnas is a ceiling like a staircase with facets and a flat roof. Every facet intersects the adjacent one at either a right angle, or half a right angle, or their sum, or another combination of these two. The two facets can be thought of as standing on a plane parallel to the horizon. Above them is built either a flat surface, not parallel to the horizon, or two surfaces, either flat or curved, that constitute their roof. Both facets together with their roof are called one cell. Adjacent cells, which have their bases on one and the same surface parallel to the horizon, are called one tier." [1]. In addition there are intermediate elements which connect the roofs of adjacent cells. (For a more detailed explanation, see the example in the following chapter.)
Al-Kashi distinguishes four types of muqarnas: The Simple Muqarnas and the Clay-plastered Muqarnas, both with plane facets and roofs, as well as the Curved Muqarnas, or Arch, and the Shirazi, in which the roofs of the cells and the intermediate elements are curved. The plane projection of a simple element (either cell or intermediate element) is a basic geometrical form, namely a square, half-square (cut along the diagonal), rhombus, half-rhombus (isosceles triangle with the shorter diagonal of the rhombus as base), almond (deltoid), jug (quarter octagon), and large biped (complement to a jug), and small biped (complement to an almond). Rectangles also occur.
The elements are constructed according to the same unit of measure, so they fit together in a wide variety of combinations. Al-Kashi uses in his computation the module of the muqarnas, defined as the base of the largest facet (the side of the square) as a basis for all proportions.
The muqarnas is used in large domes, in smaller cupola, in niches, on arches, and as an almost flat decorative frieze. In each instance the module as well as the depth of the composition is different and adapts to the size of the area involved or to the required purpose. The muqarnas is at the same time a linear system and an organization of masses.
There is a relatively unbroken tradition of architectural practice in the Islamic culture. From the Ilkhanid period until today, 700 years later, the elements mentioned above did not change, but at the same time more elaborate muqarnas were constructed in which we find elements like five-, six-, or seven-pointed stars.

Here is a link to the website with a great survey on plans of Muqarnas, ordered by there geographic and historic relations:
www.tamabi.ac.jp/idd/shiro/muqarnas/

Elements of Bastam

In this  detailed picture of a  muqarnas at Bastam (an Ilkhanid shrine situated midway between Tehran and Mashad) you see a few cells and the correlating plan. These cells consist of two facets, or vertical sides, with their curved roof. In general a roof can be a flat surface, not parallel to the horizon, or two joint surfaces, either flat or curved. The roofs of two adjacent cells can be connected by intermediate elements consisting of one surface, or two joint surfaces. A row of cells, with their bases on the same surface parallel to the horizon, is called a tier.
On the lower tier we see from right to left (in the plan: beginning at the upper right corner of the non-shaded area): an intermediate element based on a small biped, a cell based on a rhombus, then two broken intermediate elements, a cell based on a quarter octagon, an intermediate element based on a small biped, a cell based on a quarter octagon, again an intermediate element based on a small biped and a cell, with only the right facet visible, based on a quarter octagon. On the tier above: a cell based on an almond, a cell based on a quarter octagon, three cells based on an almond with a fourth one being barely visible.

Basic Geometrical Forms

The plane projections of the two different types of elements, cell and intermediate element, are simple geometrical forms. There are six such forms that are used most often: square, rhombus, almond (deltoid), jug (quarter octagon), large biped (complement to a jug) and small biped (complement to an almond).
Without context there exists no one-to-one relationship between cells, intermediate elements and their plane projections (see the rhombus example).
In the following we present the basic geometrical forms according to Al-Kashi [2, 3] and possible realizations as cells or intermediate elements. The side measuring the length of the module always lies at the bottom of each picture.

1. Square

   Square as a cell.

   
   [Animation] [VRML Model]

2. Rhombus

   Rhombus both as a cell and as an intermediate element.

   
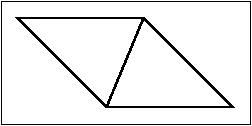
   cell: [Animation] [VRML Model] intermediate element: [Animation] [VRML Model]

3. Almond (deltoid)

   Almond as a cell.

   
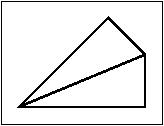
   [Animation] [VRML Model]

4. Jug

   Jug as a cell.

   
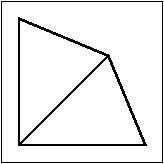
   [Animation] [VRML Model]

5. Large Biped

   Large biped as an intermediate element.

   
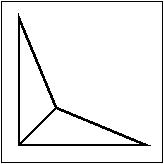
   [No Animation available] [No VRML Model available]

6. Small Biped (complement to a jug)

   Small Biped as an intermediate.

   
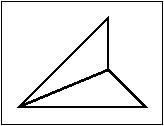
   [Animation] [VRML Model]

South Octagon Vault of the Takht-i Suleyman

The Takht-i Suleyman (Throne of Salomon) is situated in a wide valley at an altitude of approx. 2000 m, ca. 30 km North of Takab, N.W. of Tehran. The Sassanian sanctuary here flourished in the 5th and 6th century and was one of the three main fire sanctuaries. After the Islamic conquest it remained important as a Zoroastrian temple until the 9th century. In the 13th century the Ilkhanid ruler Abaqa (1265-1281) constructed a summer palace on the southern part of the ruins, partly based on the same layout and using former construction material. As the Mongol court was used to living in tents, the construction of the palace was not made for eternity and soon fell to ruins. In the ruins of the western part of the palace a plate has been found, which was recognized as a construction plan for a muqarnas vault. In analogy to this plan, Ulrich Harb proposed a possible plan to reconstruct the much simpler south octagon vault [6]. This plan is the base of our construction.

This animation [180kB] blends between Harb's plan and our construction.

---

Video Magic of Muqarnas Stalactite Vaults in Islamic Architecture Yvonne Dold-Samplonius Silvia Harmsen Susanne Krömker Michael J. Winckler Duration: 18 min Format: PAL or NTSC May 2005

We have completed the DVD/VHS with an accompanying booklet in English. Audio traces are in Arabic, English, German, Persian, and Turkish. Sorry, but we do not ship the video any more. Since January 2015, the English version is available for free via the following link www.ub.uni-heidelberg.de/archiv/17446

---